A analise de regressão linear avalia a relação estatística entre uma ou mais variáveis. Vamos exemplificar …

Quando consideramos o efeito de duas ou mais variáveis, utilizamos a análise de regressão múltipla, exemplo:

Quando consideramos o efeito de apenas 1 variável, utilizamos a analise de regressão simples. Para que serve uma regressão ?
O modelo de regressão serve para prever comportamentos com base na associação entre duas variáveis que geralmente possuem uma boa correlação.
Mas onde utilizo essa regressão?
As aplicações são diversas !! Exemplos:
- Prever o valor de fechamento de uma ação na ibovespa;
- Produtividade de colaboradores de um call center;
- % de Desmatamento nos próximos anos;
- Previsão de faturamento;
e muitos outros. Lembrando que a Estatística não é 100% assertiva, o papel dela é te direcionar.
Banco de Dados
O banco de dados utilizado nesse exemplo foi extraído do site da Kaggle.
Esses dados são referentes ao custo de seguro de saúde nos Estados Unidos. O desafio desse case é prever o custo com base nas características da pessoas.
Colunas
Idade: idade do beneficiário principal
Sexo: sexo do contratante do seguro, feminino, masculino
IMC: Índice de massa corporal, fornecendo uma compreensão do corpo, pesos que são relativamente altos ou baixos em relação à altura, índice objetivo de peso corporal (kg / m ^ 2) usando a relação entre altura e peso, idealmente 18,5 a 24,9
Filhos: Número de filhos cobertos pelo seguro saúde / Número de dependentes
Fumante: Se é fumante
Região: área residencial do beneficiário nos EUA, nordeste, sudeste, sudoeste, noroeste.
Encargos: despesas médicas individuais cobradas pelo seguro
saúde
Importando os Dados
Vamos importar a base para o Excel. Já existe funções prontas no Excel para fazer esse tipo de processo.
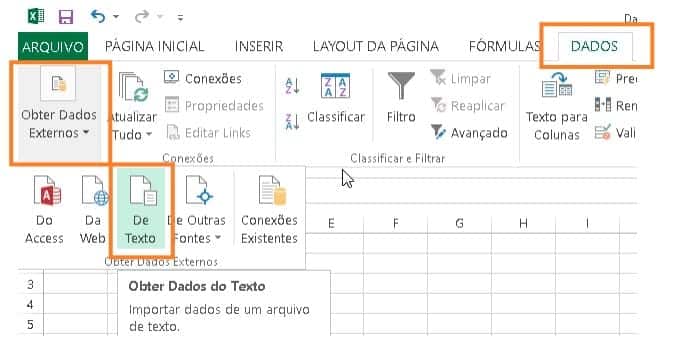
Vamos ajustar os parâmetros de importação, devido o arquivo estar em formato .CSV
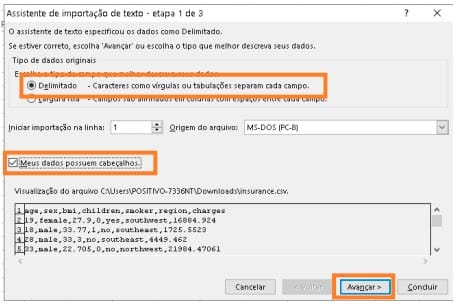
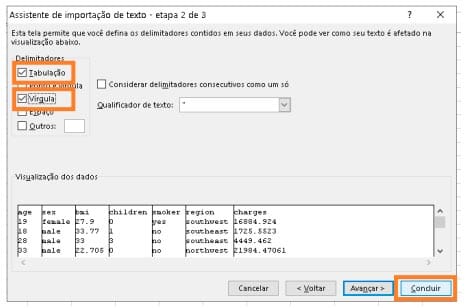
Verificando os dados
Vamos verificar os primeiros registros.

Vamos transformar os registros números em valores numéricos.
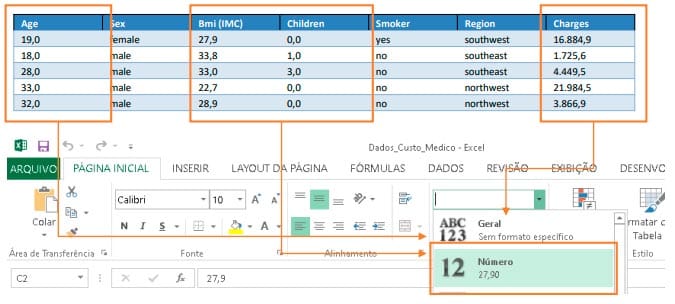
Vamos verificar se há campos em branco na base de dados.
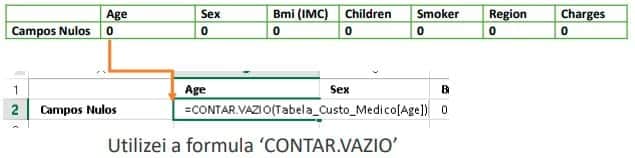
Filtrando os dados
Como estamos lidando com um problema linear, vou retirar as colunas que não forem valores numéricos. Assim vamos ficar apenas com as colunas:
- Age (Idade)
- BMI (IMC)
- Children (Filhos)
- Charges (Custo)
Agora vamos criar algumas analises gráficas das variáveis numéricas.
Custo x IMC
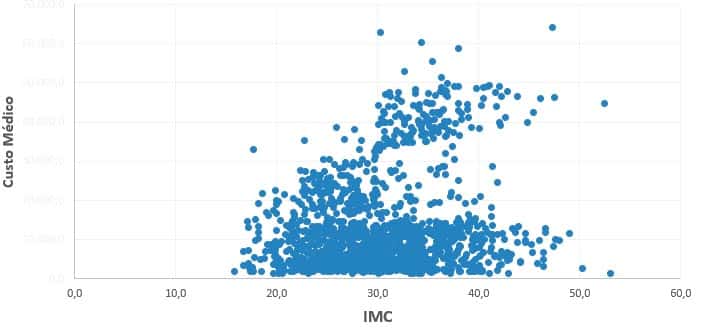
Insights sobre custo x IMC
- Há um grande público com o IMC entre 25 a 35 anos
- Poucos outliers
- Leve tendência entre IMC x Custo
Custo x Idade
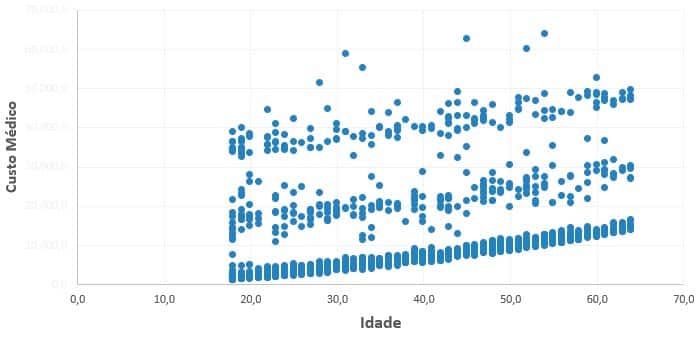
Insights sobre custo x idade
- Existe aparentemente 3 grupos de faixa de idade x preço
- Leve tendência entre Idade x Custo
Custo x Filhos
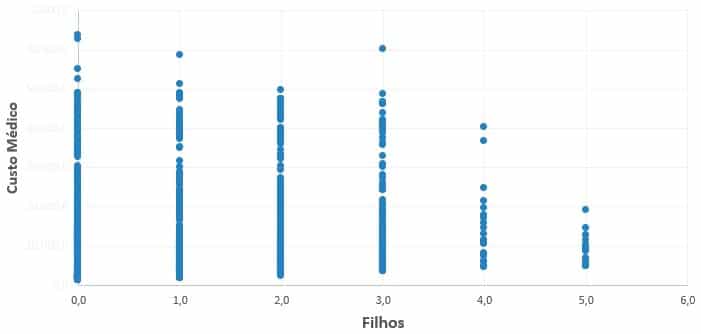
Insights sobre custo x filhos
- Maior concentração tem até 2 filhos
- Aparentemente não há tendência entre Idade x Custo
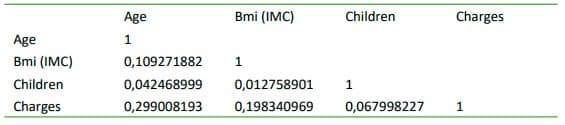
Vamos calcular a correlação entre essas variáveis
Para criar essa tabela siga essa rotina:
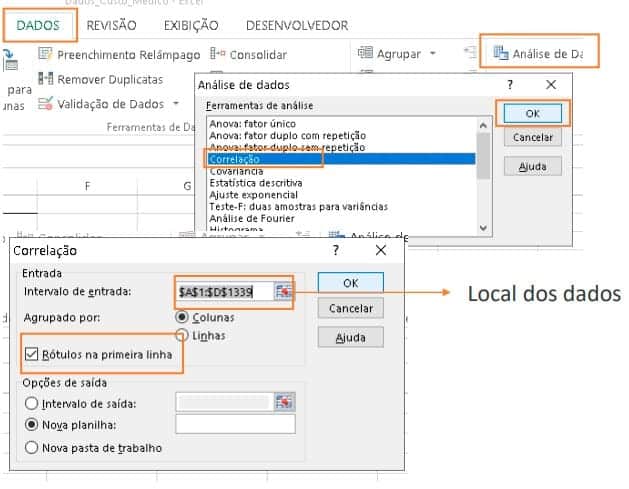
Vamos entender a tabela de correlação
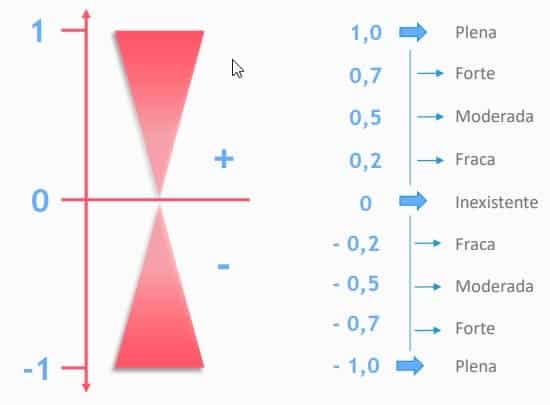
A correlação pode ser positiva ou negativa, sendo que a escala vai de 1 a -1.
Quanto mais próximo de 1, há uma correlação positiva, ou seja, quando uma variável cresce a outra cresce.
Quanto mais próxima de -1, há uma correlação negativa, ou seja, quando uma variável cresce a outra diminui ou vice-versa.
No nosso exemplo as correlações ficaram em 0.29, 0.19, 0.0 ou seja, não há uma correlação forte entre as variáveis.
Na regressão é sempre importante haver correlações fortes entre as variáveis. Caso não haja, o modelo irá ter uma dispersão muito grande e as previsões ficarão fora da realidade.
Vamos entender o custo médico
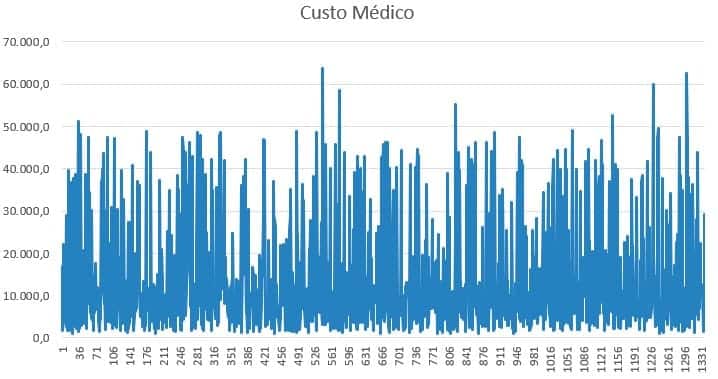
Análise estatística:
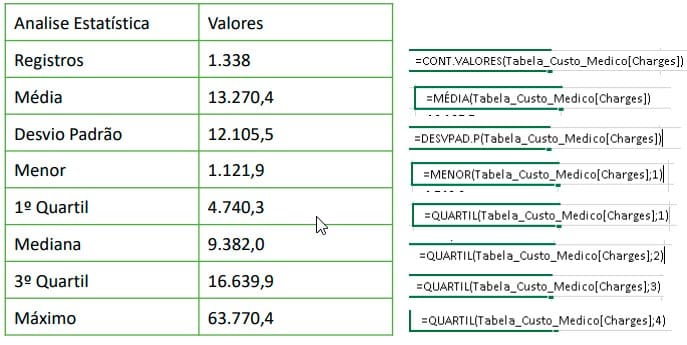
Foram utilizadas as fórmulas:
- Cont.valores
- Média
- Desvpad.p
- Quartil
- Menor
Insights sobre a análise estatística
A média do ‘custo médico’ fica acima da mediana e o desvio padrão esta com grande oscilação, ou seja, há um range muito grande no ‘custo médico’.
Vamos criar a regressão linear!
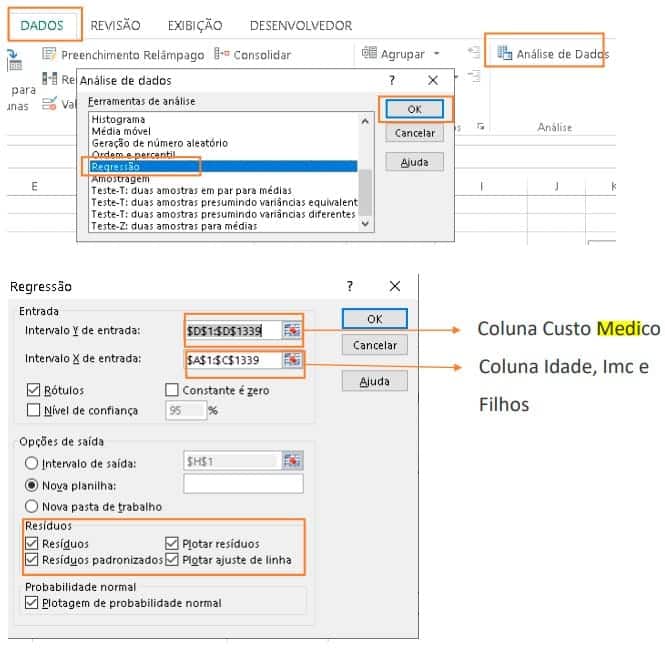
Fórmula da regressão linear:
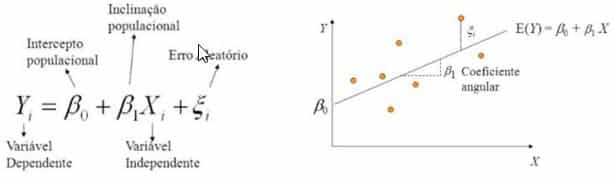
Caso não tenha conhecimento sobre estatística, segue um vídeo bem legal de como funciona essa formula.
Avaliando o modelo
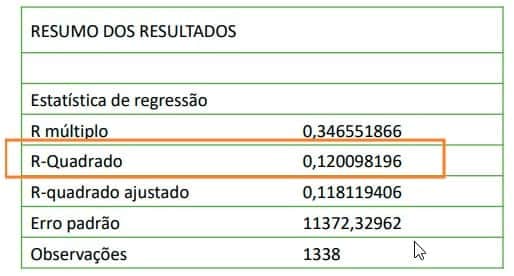
A definição do R-quadrado é bastante simples: é a porcentagem da variação da variável resposta que é explicada por um modelo linear.
O R-quadrado está sempre entre 0 e 100%:
0% indica que o modelo não explica nada da variabilidade dos dados de resposta ao redor de sua média.
100% indica que o modelo explica toda a variabilidade dos dados de resposta ao redor de sua média.
Ou seja, nosso modelo não houve uma performance aceitável. Nesse caso iremos ter que pesquisar novos dados para incluir no modelo e treinar novamente o modelo.


